5x5x5-ös bűvös kocka kirakása egyszerűen
Ha kíváncsi vagy megleled a talányokat magad
körül. Ha eltökélt is vagy megoldod azokat."
If you are curious, you'll find the puzzles around you.
If you are determined, you will solve them. (E. Rubik)
Az 5x5x5-ös bűvös kocka kirakása
Jelen leírás egy jó nagyra nőtt Rubik-kocka, az 5x5x5-ös bűvös kocka (Professor's Cube) kirakásáról szól. A különböző kockák megoldásáról számtalan leírás és videó található az Interneten. A jelen leírásban azoknak a kocka-kedvelőknek igyekszünk segítséget nyújtani akik már megbarátkoztak a 3x3-as illetve a 4x4-es kockával és szeretnék megoldani egyszerűen az 5x5x5-ös kockát is.
A 3x3x3-as és a 4x4-es bűvös kockák kirakására vonatkozó módszerünk megismerésével, minimális gyakorlással (akár újabb forgatás-sorozat megtanulása nélkül) bármikor, bárki ki tudja rakni az 5x5x5-ös kockát is, anélkül, hogy rendszeresen órákig kellene gyakorolnia a forgatásokat.
Tudni kell, hogy a kockát forgató versenyzők (speedcuberek), akik néhány másodperc alatt rakják ki a Rubik-kockát (a nagyobbakat is 1-2 perc alatt) több száz forgatássorozatot ismernek és az adott kockaállapothoz a megfelelőt a másodperc töredéke alatt tudják azonosítani és végrehajtani.

A bűvös kockákról további információkat a linkgyűjteményben talál

A forgatásokhoz használt (módosított) jelölőrendszerünk leírását és egy mini-lexikont itt találhat.
Az 5x5x5-ös bűvös kocka rendezésének menete:
- Először a lapközepeken található 6x9 színes kiskockákat rendezzük oldalanként egy színűre,
- majd a - rendezetlen kockán szétszórva található (12x3 db) élkockákat rakjuk szín szerint hármas csoportokba.
- A kétféle forgatássorozat eredményes befejezése
után hozzájutunk egy - lényegében - 3x3-as Rubik-kockához,
aminek a kirakását már ismerjük vagy itt megtekinthetjük.
1. Lapközepek rendezése
Itt a feladatunk az, hogy az oldalak közepén található 6x9 db egyszínű kiskockát oldalanként egy színűre, egymás mellé forgassuk. Itt is, mint a 3x3x3-as kockánál, a középen levő kiskockák meghatározták az adott oldal színét, mert egymáshoz képest állandó a helyzetük. A lapközepek hatékony rendezése érdekében azonban érdemes ismernünk a kockán lévő színek egymáshoz képesti helyzetét.
A jobb áttekinthetőség érdekében a kocka-rajzokon szürke színű kiskockákat is láthatunk, ezek az adott forgatásokban érdektelenek vagy szerepük nincs.
A lapközepek rendezése intuitív módon, egyszerűen megoldható, komolyabb segítséget nem igényel annak, aki már egy kis tapasztalatot szerzett a 3x3-as és 4x4-es kockák kirakása során.
Praktikus okokból mindig azonos pl. fehér vagy citromsárga oldallal kezdjük a lapközepek rendezését, mert ezek a színek - ha jó a kocka színezése - könnyebben szembe tűnnek. Az első lapközép rendezése után a szemben levő oldal lapközepét rakjuk ki. Ezután a két kirakott lapközepes oldalnál fogjuk meg a kockát és már csak a fennmaradó négy oldal irányában forgatva a kockát rakjuk ki a további négy lapközepet. Célszerű a lapközepek kiskockáiból kettes vagy hármas "csíkokat" összeállítani és a fennmaradó négy oldal síkjában mozgatni és rendezni a közepeket színek szerint.
A lapközepek rendezése intuitív módon megoldható annak, aki már egy kis tapasztalatot szerzett a kisebb kockákkal. Ezért ehhez nem is írunk részletes algoritmusokat. Kezdőknek gondot okozhat egy-két befejező forgatás, ezekre alábbiakban mutatunk megoldásokat:
1.1 Három-kockás helyzet

Rendező algoritmus: Ru - de - Ru - do
1.2 Két-kockás helyzet

Rendező algoritmus: Re - de - Ro - do
Lehetne még további "két-kockás" helyzeteket ábrázolni és forgatásokat is szerkeszteni hozzá, de bízunk az olvasó kirakási intuicióiban. Ha mégis gondot okozna a kirakásuk csinálj a rossz hármasokkal egy 1.1 forgatást, ezzel hozzájutsz valamelyik "egy-kockás" helyzethez.
1.3 Egy-kockás helyzet(1)
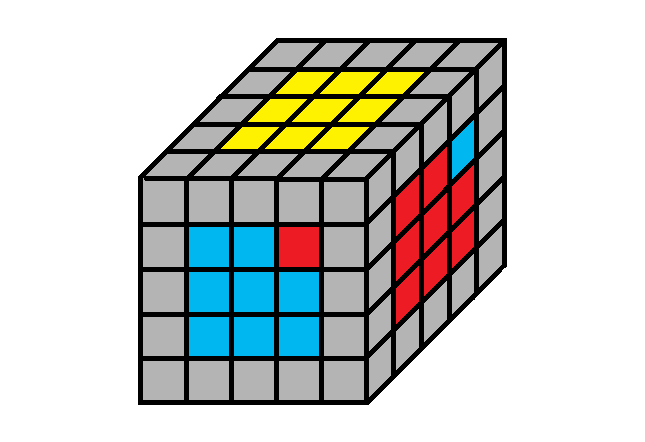
Rendező algoritmus : te - Fe - do - Fo - to - Fe - de
1.3.2 Egy-kockás helyzet(2)

Rendező algoritmus: Ho - Fe - do - Fo - He - Fe - de
Az előző algoritmusokat nem szükséges memorizálni, némi gyakorlás után készséggé vál(hat)nak. A lapközepeken található 9 (pontosabban 8) közép-kiskocka bármelyike az előző két algoritmussal helyre hozható, csak az "F" és "R" oldal megfelelő elforgatásával be kell állítanunk az ábrán látható valamelyik induló pozíciót.
Figyeljük meg, hogy mi történik a két utóbbi - kissé bonyolultnak tűnő - forgatás során: (Jelöljük a két kicserélendő kiskockát A (a piros) ill. B (a kék) betűvel.) Először a B kockát (tartalmazó réteget) az A kocka helyére visszük (1. fordítás), ezután oldalra fordítjuk és kivisszük az F oldalról a B kockával feltöltött sort (2) és (3), ezután visszafordítjuk az F oldalt (4), majd az első lépésben kiforgatott réteget is visszaforgatjuk (5), az F oldalt harmadszor is elfordítjuk (6), hogy befejezhessük a rendezést (7). Teljesen áttekinthető a folyamat, ezért egy átlagos térlátású kockaforgatónak nem is kell memorizálnia ezeket a forgatássorozatokat.
Elkészülnek tehát a lapközepek:

2. Élkockák rendezése
Feladatunk a rendezetlen kockán szétszórva található 12x3=36 élkocka szín szerint hármas csoportokba való rendezése. Kissé aprólékos és némi türelmet igénylő munka, de a 4x4-es kocka élpárosításánál megismert egyszerű és áttekinthető forgatássorozat ismételgetésével nagyrészt célt érhetünk.
Állítsuk be a két egymás mellé beforgatandó (párosítandó) élkockát úgy, hogy mindkettő a felső lapra (T) kerüljön. Egyik velünk szemben (T és F oldal találkozásánál), a másik túloldalt, a T és B oldal találkozásánál legyen. (Az ábrán a fekete színnel jelzett két élkocka.) Ügyeljünk arra, hogy a két beforgatandó élkocka színeiket tekintve megfelelő állásba kerüljön, vagyis a forgatássorozat végén a kész élkockapár színei oldalról tekintve azonosak legyenek. A forgatássorozatban mellékes szerepet játszó három élkockának (nevezhetjük ezeket segédélkockáknak) még nem rendezett élkocka-hármast válasszunk! Lásd: ábra.

Javasolt forgatássorozat (ugyanaz, mint a 4x4-esnél): li-To-Ri-Ti-lo
Ha a T és B oldal találkozásánál levő közép-élkockát párosítanánk, akkor a forgatás-sorozat értelemszerűen: Mi-To-Ri-Ti-Ma.
Az élkockák párosításának variációi még: a közelebbi élkockát visszük fel, a bal oldalon helyezzük biztonságba a
párosított élkockákat, stb.
Figyeljük meg, hogy mi történik a forgatások során: Először párosítjuk a kiválasztott élkockákat (1. fordítás), ezután oldalra visszük (2) és "biztonságba" helyezzük (3), majd miután a segédélkockák a helyükre léptek, visszafordítjuk a felső réteget (4), hogy az elmozdított lapközepeket helyre hozhassuk (5). Teljesen áttekinthető a folyamat, ezért egy átlagos térlátású kockaforgatónak nem is kell memorizálnia ezt a forgatássorozatot.
3. Élkockák rendezésének végén felmerülő paritás helyzetek
Az 5x5x5-ös kocka rendezése során már az élhármasok kialakítása során beleütközünk paritás-helyzetekbe. A továbbiakban ezeket vesszük sorra.
Tippek, lehetőségek:
Az élhármasok rendezése során először olyan élekhez keressünk harmadikat, amiben kettő élkocka már színeiben és orientációban is megfelelő, ha találunk ilyeneket.
Amikor már csak néhány rendezendő élhármas maradt törekedjünk arra, hogy olyan élhármasokat hozzunk létre, amelyben a két szárny színezése azonos. Ha az élhármasok kialakításának vége felé pontosan három ilyen (még nem rendezett) élhármas marad és egyik hármas sem tartalmaz három azonos színösszeállítású élkockát, akkor nagyrészt elkerülhetjük a paritások alkalmazását. Ezeket megfelelően orientálva beállítjuk az ismertetett forgatásorozat kiinduló helyzetébe és végrehajtva a forgatásokat, mind a 12 élhármasunk rendezett lesz. Mint láthatjuk, ez utóbbi esetben egyszerre három élhármast tudunk rendezni.
Természetesen sokszor előfordul olyan eset, hogy a rendezés végén a legutolsó élhármas színe nem megfelő, mert az élközép-kocka a szárnykockákhoz képest fordított állású. Ekkor szükségünk van a 3.1 pont szerinti algoritmus alkalmazására.
Az is megtörténhet, hogy a rendezés végén két élhármasban egyes kiskockák színe nem megfelő, mert az adott kiskockák a másik élsorban helyezkednek el. Ekkor szükségünk van a 3.2 vagy a 3.3 pont szerinti algoritmus alkalmazására.
A segédélkockák és az ún. társkockák színösszeállítása és orientációja függvényében - jó esetben - egyszerre egy, kettő vagy három élhármast tudunk rendezni.
3.1 Az utolsó élhármas színezése nem homogén

Alkalmazandó forgatás-sorozat:
ru-Bu-Tu-le-Tu-ro-Tu-re-Tu-Fu-re-Fu-lo-Bu-ru
Ez egy 15 fordításból álló algoritmus, ezért szükséges, hogy egy kicsit egyszerüsítsük és könnyen megjegyezhető alakra hozzuk, mert elég gyakran szükségünk van rá.
Vegyük észre, hogy a T, F és B oldalak mindig félfordulatot végeznek, ezen kívül csak az "r" illetve az "l" rétegek fordulnak. Egyszerűsítések után szerkeszthető egy olyan, megjegyezhető szavakból kialakuló szósorozat, amelyben csak az r és l betűk utáni magánhangzó releváns és jelzi a forgatás irányát, míg a "T", "F" és "B" utáni magánhangzóknak nincs jelentőségük, mert úgyis mindig félfordulat következik. (A zárójelben lévő betűknek sincs jelentőségük, mert amúgy sem szerepelnek a forgatásokhoz használt jelölőrendszerünkben.)
A forgatássorozat az előzőekben leírt értelmezéssel memorizálható így is:
Rubi(n)t letörő töret. Férfi lábo(n) rú(g).
(ugyanaz, mint a 4x4x4-es kockánál)
3.2 Két élhármasban egy-egy szárnyat kell megcserélni

Alkalmazandó forgatás-sorozat:
(lo-Tu)2-Fu-lo-Fu-re-Tu-ro-Tu-lu
Az algoritmus végrehajtása eredményeként a feketével jelzett élszárnyak egymással kicserélődnek és meg is fordulnak.
A forgatássorozat az előzőekben leírt egyszerűsítésekkel (az "r" és "l" rétegekre megadott forgásirány releváns, T és F oldal mindig
félfordulatot végez, ezért a rájuk vonatkozó forgásirány-jelölés irreleváns) és értelmezéssel memorizálható így is:
Lótu(sz), lótu(sz)-faló, fűré(sz)t ro(s)tálu(nk).
(ugyanaz, mint a 4x4x4-es kockánál)
Ha csak saját kedvünkre forgatjuk a kockát és az idő nem számít, akkor nem szükséges az itt következő paritás-algoritmust tudni, elég az előző kettőt ismerni ahhoz, hogy meg tudjuk oldani az összes paritás helyzetet.
3.3 Két élhármasban az élközepeket kell megcserélni

Alkalmazandó forgatás-sorozat:
ru-Bu-(ro-Tu)2-Bu-ro-Bu-re-Bu-ro-Bu-ru-Bu-Tu
A forgatás-sorozat eredményeként a feketével jelzett közép-élkockák egymással kicserélődnek.
Megjegyzés: Az algoritmus végrehajtásával a közép-élkockák megfordulás nélkül helyezdődnek át, azonban "mellékhatásként" a közelebbi szárnyak egyúttal meg is fordulnak. (A kirakás ezen fázisában ez azonban semmi gondot nem okozhat.)
Nem szükséges ezt az algoritmust megtanulni, mert kiváltható kétszer végrehajtott 3.2-es forgatással, közötte az egész kocka függőleges tengelyű 180°-os transzformációjával.
Ha valaki mégis meg kívánja tanulni ezt a forgatássorozat is, az előzőekben leírt egyszerűsítésekkel (T és B oldal mindig
félfordulatot végez, stb.) és értelmezéssel memorizálható így is:
Rubi(n), rőt, rőt, bíró bére boro(k), berú(g), bete(g).
4. A kocka rendezése
Az előző három fejezet végrehajtása után kialakítottunk egy lényegében 3x3x3-as Rubik-kockát,

aminek a kirakását már ismerjük vagy itt megtekinthetjük.
Talán azt nem is kell említeni, hogy ebben a befejező fázisban az 5x5-ös kocka külső oldalait csak magukban, a kocka belső három rétegét pedig együtt forgassuk.
Megjegyzés: Ebben az utolsó fázisban már nem találkozunk újabb paritáshelyzetekkel, mint ahogy az a 4x4x4-es vagy 6x6x6-os kockáknál előfordulhat.
Ha a fenti forgatássorozatok rendben megtörténtek, akkor örülhetünk a kész 5x5x5-ös kockánknak.
Összeállította: Straub Tamás
A leírt módszer - részben vagy egészben - a forrás megjelölésével szabadon felhasználható.
Írjon nekünk, ha a portállal vagy az oldallal kapcsolatban mondanivalója van:



