6x6x6-os bűvös kocka kirakása egyszerűen
Ha kíváncsi vagy megleled a talányokat magad
körül. Ha eltökélt is vagy megoldod azokat."
If you are curious, you'll find the puzzles around you.
If you are determined, you will solve them. (E. Rubik)
Az 6x6x6-os bűvös kocka kirakása

A leírás egy óriásira nőtt bűvös kocka (Rubik-kocka), a 6x6x6-os kocka kirakásáról szól. A különböző kockák kirakásáról számos leírás és videó található az Interneten. A jelen leírásban azoknak a kocka-kedvelőknek igyekszünk segítséget nyújtani akik már megbarátkoztak a 3x3-as illetve a 4x4-es kockával (esetleg az 5x5x5-ös kockával is) és szeretnék megoldani az 6x6x6-os kockát is.
A 3x3x3-as, a 4x4-es és 5x5-ös bűvös kockák kirakására vonatkozó módszerünk megismerésével, minimális gyakorlással (akár újabb forgatás-sorozat megtanulása nélkül is) bármikor, bárki ki tudja rakni a 6x6x6-os bűvös kockát is, anélkül, hogy rendszeresen órákig kellene gyakorolnia a forgatásokat.
Tudni kell, hogy a kockát forgató versenyzők (speedcuberek), akik néhány másodperc alatt rakják ki a Rubik-kockát (a nagyobbakat is 1-2 perc alatt) több száz forgatássorozatot ismernek és az adott kockaállapothoz a megfelelőt a másodperc töredéke alatt tudják azonosítani és végrehajtani.

A forgatásokhoz használt (módosított) jelölőrendszerünk leírását és egy mini-lexikont itt találhat.
A 6x6x6-os bűvös kocka rendezésének menete:
- Először a lapközepeken található (6x16) 96 színes kiskockákat rendezzük oldalanként egy színűre,
figyelve az oldalak színsorrendjére,
- majd a - rendezetlen kockán szétszórva található - (12x4) 48 db élkockákat rakjuk szín szerint
négyes sorokba.
- A kétféle forgatássorozat eredményes befejezése után hozzájutunk egy rendezetlen, lényegében
3x3-as kockához, ahol az élnégyesek adják a Rubik-kocka élkockáit, a 16 kiskockából
álló oldalközepek pedig a középkockákat,

aminek a kirakását már ismerjük vagy itt megtekinthetjük.
1. Lapközepek rendezése
Itt a feladatunk az, hogy az oldalak közepén található 6x16 db egyszínű kiskockát oldalanként egy színűre, egymás mellé forgassuk. Most nincs olyan támpontunk, mint a 3x3x3-as (vagy 5x5x5-ös) kockánál, ahol a középen levő kiskockák meghatározták az adott oldal színét, mert egymáshoz képest állandó a helyzetük. A lapközepek hatékony és megfelelő rendezése érdekében tehát készségszinten kell ismernünk a kockán lévő színek egymáshoz képesti helyzetét.
A lapközepek rendezése intuitív módon, egyszerűen megoldható, komolyabb segítséget nem igényel annak, aki már egy kis tapasztalatot szerzett a 3x3-as, 4x4-es és 5x5-ös kockák kirakása során.
Praktikus okokból mindig azonos pl. fehér vagy citromsárga oldallal kezdjük a lapközepek rendezését, mert ezek a színek - ha jó a kocka színezése - könnyebben szembe tűnnek. Az első lapközép rendezése után a szemben levő oldal lapközepét rakjuk ki. Célszerű ezután a két kirakott lapközepes oldalnál megfogni a kockát és ezután már csak a fennmaradó négy oldal irányában forgatva a kockát rakjuk ki a további négy lapközepet. Célszerű az egymás melletti oldalközepek kirakásával folytatni úgy, hogy a lapközepek kiskockáiból hármas vagy négyes "csíkokat" állítunk össze és a fennmaradó négy oldal síkjában mozgatjuk, cserélgetjük és rendezzük a közepeket színek szerint, figyelve a színek egymáshoz viszonyított helyzetére is.
A lapközepek rendezése intuitív módon megoldható annak, aki már egy kis tapasztalatot szerzett a kisebb kockákkal. Ezért ehhez nem is írunk részletes algoritmusokat. Kevésbé gyakorlott kockaforgatóknak gondot okozhat egy-két befejező forgatás, ezekre alábbiakban mutatunk megoldásokat:
1.1 helyzet
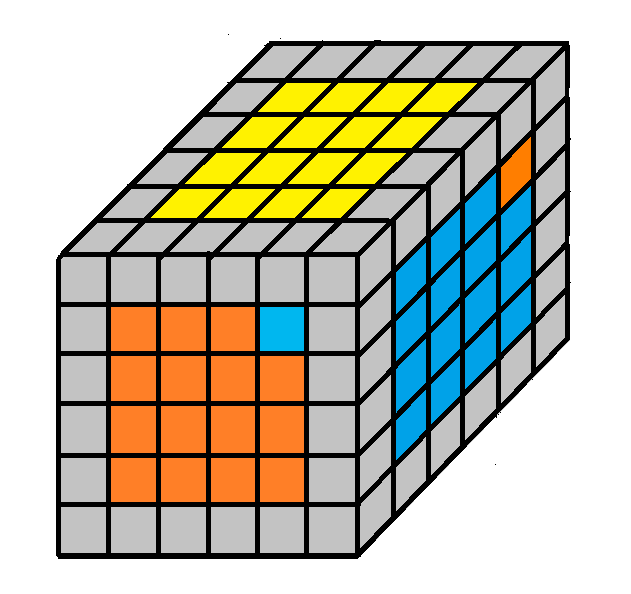
Rendező algoritmus:
2Te - Fe - 2Da - Fo - 2To - Fe - 2De
1.2 helyzet
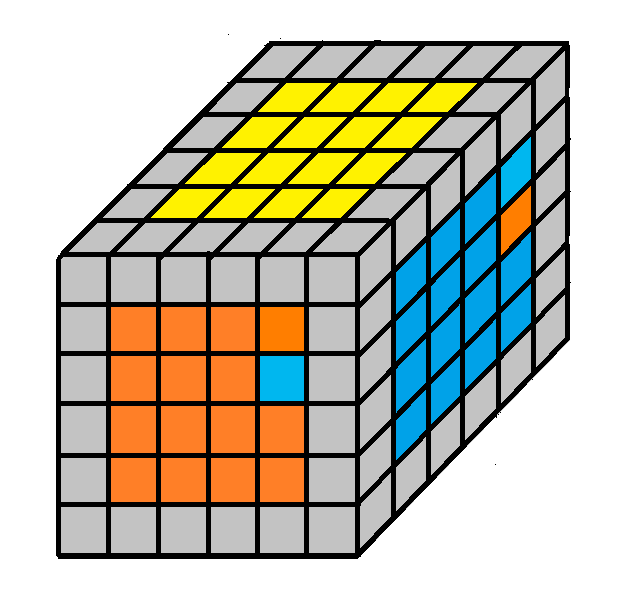
Rendező algoritmus:
3Te - Fe - 2Da - Fo - 3To - Fe - 2De

Rendező algoritmus:
3Do - Fe - 2Do - Fo - 3De - Fe - 2De

Rendező algoritmus:
3Te - Fe - 3Do - Fo - 3To - Fe - 3De
Az utolsó két lapközép intuitív rendezése során általában egy-két kiskocka megmarad, aminek szinezése a másik oldal szerinti. Ezeket egyesével a fenti algoritmusokkal rendezhetjük. Az oldalakon található 16 közép-kiskocka bármelyike a fenti négy algoritmussal helyre hozható, csak az "F" és "R" oldal megfelelő elforgatásával be kell állítanunk az ábrán látható valamelyik induló pozíciót.
Figyeljük meg, hogy mi történik minden forgatás során: (Jelöljük a két kicserélendő kiskockát A (a kék) ill. B (a narancs színű) betűvel.) Először a B kockát (tartalmazó réteget) az A kocka helyére visszük (1. fordítás), ezután oldalra fordítjuk és kivisszük az F oldalról a B kockával feltöltött sort (2) és (3), ezután visszafordítjuk az F oldalt (4), majd az első lépésben kiforgatott réteget is visszaforgatjuk (5), az F oldalt harmadszor is elfordítjuk (6), hogy befejezhessük a rendezést (7). Teljesen áttekinthető a folyamat, ezért egy átlagos térlátású kockaforgatónak nem is kell memorizálnia ezeket a forgatássorozatokat.
Elkészülnek tehát a lapközepek:
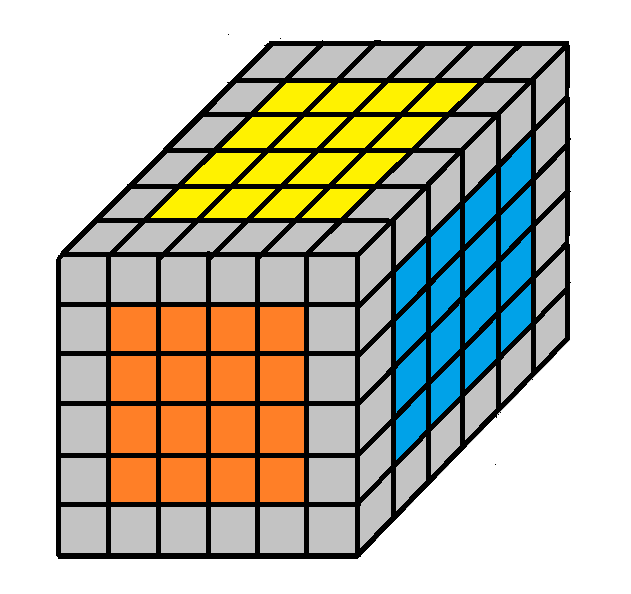
2. Élkockák rendezése
Ebben a fázisban feladatunk a rendezetlen kockán szétszórva található 12x4=48 élkocka szín szerint négyes csoportokba való rendezése. Aprólékos és igen nagy türelmet igénylő munka, de a 4x4-es vagy 5x5-ös kocka éleinek rendezésénél megismert egyszerű és áttekinthető forgatássorozat ismételgetésével nagyrészt célt érhetünk.
Állítsuk be az egymás mellé beforgatandó (rendezendő) élkockákat úgy, hogy mindegyik a felső lapra (T) kerüljön. Amelyekhez társítani akarunk azok velünk szemben a (T és F oldal találkozásánál), a beforgatandó(k) túloldalt, a T és B oldal találkozásánál legyen(ek). (Az ábrán a fekete színnel jelzett élkockák.) Ügyeljünk arra, hogy a beforgatandó élkockák színeiket tekintve megfelelő állásba kerüljenek, vagyis a forgatássorozat végén az új élkockasor színei oldalról tekintve azonosak legyenek. A forgatássorozatban mellékes szerepet játszó négy élkockának (nevezhetjük ezeket segédélkockáknak) még nem rendezett élkocka-sort válasszunk! Lásd: ábra.

Javasolt forgatássorozat (hasonló, mint a kisebbeknél):
3Ro-Te-Ri-To-3Re
Ha a T és B oldal találkozásánál levő másik élkockát párosítanánk, akkor a forgatás-sorozat értelemszerűen módosul.
Az élkockák párosításának variációi még: a közelebbi élkockát visszük fel, a bal oldalon helyezzük biztonságba a
párosított élkockákat, stb.
Ha már egy kis gyakorlatot szereztünk az élnégyesek kialakítása során, gyorsíthatjuk a sorok kirakását úgy, hogy megfigyeljük a
forgatássorozatban a segédélkockákból melyik és hogyan csatlakozik a társélkockákhoz.
Figyeljük meg, hogy mi történik a forgatások során: Először párosítjuk a kiválasztott élkockákat (1. fordítás), ezután oldalra visszük (2) és "biztonságba" helyezzük (3), majd miután a segédélkockák a helyükre léptek, visszafordítjuk a felső réteget (4), hogy az elmozdított lapközepeket helyre hozhassuk (5). Teljesen áttekinthető a folyamat, ezért egy átlagos térlátású kockaforgatónak nem is kell memorizálnia ezt a forgatássorozatot.
3. Élkockák rendezésének végén felmerülő paritás helyzetek
A 6x6x6-os kocka rendezése során már az élnégyesek kialakítása végén beleütközünk paritás-helyzetekbe. A továbbiakban ezeket vesszük sorra.
Tippek, lehetőségek:
Az élsorok rendezése során először olyan élekhez keressünk beillesztendő élkockát, amiben kettő vagy három élkocka már színeiben és orientációban is megfelelő, ha találunk ilyeneket.
Amikor már csak néhány rendezendő élnégyes maradt törekedjünk arra, hogy olyan élnégyeseket hozzunk létre, amelyben a két szárny ill. a két élközép-kockák színezése azonos vagy más módon szimmetrikusak a fennmaradó élsorok. Ha az élsorok kialakításának vége felé pontosan három ilyen (még nem rendezett) élnégyes marad és egyik sor sem tartalmaz négy azonos színösszeállítású élkockát, akkor időnként elkerülhetjük a paritások alkalmazását. Ezeket megfelelően orientálva beállítjuk az ismertetett forgatásorozat kiinduló helyzetébe és végrehajtva a forgatásokat, mind a 12 élnégyesünk rendezett lesz. Mint láthatjuk, ez utóbbi esetben egyszerre három élsort tudunk rendezni.
Természetesen sokszor előfordul olyan eset, hogy a rendezés végén a legutolsó élnégyes színe nem megfelő, mert az élközép-kockák a szárnykockákhoz képest fordított állásúak. Ekkor szükségünk van a 3.1 pont szerinti algoritmus alkalmazására.
Az is előfordul, hogy a rendezés végén két élnégyesben egyes kiskockák színe nem megfelő, mert az adott kiskockák a másik élnégyesben helyezkednek el. Ekkor szükségünk van a 3.2 vagy a 3.3 pont szerinti algoritmus alkalmazására.
A segédélkockák és az ún. társkockák színösszeállítása és orientációja függvényében egyszerre egy, kettő vagy három élnégyest tudunk rendezni.
3.1 Az utolsó élnégyes színezése nem homogén

Alkalmazandó forgatás-sorozat:
2Ru-Bu-Tu-2Le-Tu-2Ro-Tu-2Re-Tu-Fu-2Re-Fu-2Lo-Bu-2Ru
Ez egy 15 fordításból álló algoritmus ezért szükséges, hogy egy kicsit egyszerüsítsük és megjegyezhető alakra hozzuk, mert elég gyakran szükségünk van rá.
Vegyük észre, hogy a T, F és B oldalak mindig félfordulatot végeznek, ezen kívül csak a "2R" és a "2L" oldalak/rétegek fordulnak. Tehát - csak ebben és a következő két algoritmusban - az adott második réteget értjük az R vagy r illetve az L vagy l betű alatt. Ezen egyszerűsítések után szerkeszthető egy olyan, megjegyezhető szavakból kialakuló szósor, amelyben csak az R és L betűk utáni magánhangzó releváns és jelzi a forgatás irányát, míg a "T", "F" és "B" utáni magánhangzóknak nincs jelentősége, mert úgyis mindig félfordulat következik. (A zárójelben lévő betűknek sincs jelentőségük, mert amúgy sem szerepelnek a forgatásokhoz használt jelölőrendszerünkben.)
Az algoritmus a leírt értelmezéssel memorizálható a már ismert formulával:
Rubi(n)t letörő töret. Férfi lábo(n) rú(g).
3.2 Két élnégyesben egy-egy élkockát kell megcserélni

Alkalmazandó forgatás-sorozat:
(2Lo-Tu)2-Fu-2Lo-Fu-2Re-Tu-2Ro-Tu-2Lu
Az algoritmus végrehajtása eredményeként az ábra szerinti - sorba nem illeszkedő, azonos poziciójú - élkockák egymással kicserélődnek és meg is fordulnak.
Előfordul, hogy nem az ábra szerinti, hanem pl. a mellette levőt kellene megcserélni, ekkor az algoritmus értelemszerű és könnyű módosításával végezzük a forgatásokat.
A forgatássorozat a 3.1 pontban leírt egyszerűsítésekkel (T és F oldal mindig félfordulatot végez, az adott belső réteget
értjük az R vagy r illetve az L vagy l betű alatt, stb.) és értelmezéssel memorizálható a már ismert formulával:
Lótu(sz), lótu(sz)-faló, fűré(sz)t ro(s)tálu(nk).
Ha csak saját kedvünkre forgatjuk a kockát, akkor nem szükséges az itt következő paritás-algoritmust tudni, elég az előző kettőt ismerni ahhoz, hogy meg tudjuk oldani az összes lehetséges paritás-helyzetet.
3.3 Két élnégyesben az élközepeket kell megcserélni

Alkalmazandó forgatás-sorozat:
2Ru-Bu-(2Ro-Tu)2-Bu-2Ro-Bu-2Re-Bu-2Ro-Bu-2Ru-Bu-Tu
A forgatás-sorozat eredményeként a két közép-élkocka pár egymással kicserélődik.
Megjegyzés: Az algoritmus végrehajtásával a közép-élkockák megfordulás nélkül helyezdődnek át, azonban "mellékhatásként" a közelebbi szárnyak egyúttal meg is fordulnak.
Ha csak saját kedvedre forgatod a kockát és az idő nem számít, akkor nem szükséges ezt az algoritmust megtanulni, mert kiváltható kétszer végrehajtott 3.2-es forgatással, közötte az egész kocka függőleges tengelyű 180°-os transzformációjával.
A forgatássorozat a 3.1 pontban leírt egyszerűsítésekkel (T és B oldal mindig félfordulatot végez, az adott második réteget
értjük az R vagy r illetve az L vagy l betű alatt, stb.) és értelmezéssel memorizálható így is:
Rubi(n), rőt, rőt, bíró bére boro(k), berú(g), bete(g).
4. A kocka rendezése
Az előző három fejezet végrehajtása után kialakítottunk egy lényegében 3x3x3-as Rubik-kockát,

aminek a kirakását már ismerjük vagy itt megtekinthetjük.
Talán azt nem is kell említeni, hogy ebben a befejező fázisban az 6x6-os kocka külső oldalait csak magukban, a kocka belső négy rétegét pedig együtt forgatjuk.
5. A kocka kirakásának végén előforduló paritások kezelése
A kocka rendezésének ebben a fázisában a paritásoknak két alapesete lehetséges:
- kettő élkockanégyest kellene egymás között kicserélni, és/vagy
- már csak egy élsor van fordított helyzetben.
5.1 A két kicserélendő élkocka-négyes egymással szemben helyezkedik el (lásd: ábra). Az alábbi forgatássorozattal egymás között
- színtartó módon - kicserélődik:
(3Ru2Ru-Tu)2-3Tu2Tu-3Ru2Ru-3Tu2Tu

A forgatás eléggé egyszerű, könnyen megjegyezhető, memoritert nem szükséges rá készíteni és már ismerhetjük a 4x4x4-es kocka kirakásából. (Mindig félfordulat történik, a "3R" és "2R" réteget együtt és három alkalommal, a "T" oldalt ill. a "2T" és "3T" réteg együttesét kétszer-készer fordítjuk meg.)
Előfordul, hogy a két kicserélendő élkockanégyes nem szemben, hanem egymáshoz képest oldalt helyezkedik el, mint az alábbi ábra is mutatja:

Ekkor is használható az előbbiekben megismert forgatássorozat, azonban előtte egy konjugálást kell végrehajtani. Algoritmusa pl.: To-Bi-Ti-Bo. Ezután következik a már ismert - (3Ru-2Ru-Tu)2-2Tu-3Tu-3Ru-2Ru-2Tu-3Tu - forgatás-sorozat. A végén újabb forgatás-sorozattal - az első inverzével - hozzuk helyre a kockát: Bi-To-Bo-Ti
5.2 Egy élkocka-négyes, amely az ábra szerinti helyzetet foglalja el az alábbi forgatássorozattal helyben megfordul:
3Ru2Ru-Bu-Tu-3Le2Le-Tu-3Ro2Ro-Tu-3Re2Re-Tu-Fu-3Re2Re-Fu-3Lo2Lo-Bu-3Ru2Ru

Bizony, ez egy 22 fordításból álló, nem könnyen memorizálható forgatássorozat, de elég gyakran szükségünk van rá, ezért célszerű
megjegyezhető formára hozni. Vegyük észre, hogy a T, B és F oldalak mindig félfordulatot végeznek, ezen kívül csak az "3L" és "2L"
ill. a "3R" és "2R" réteg fordul, mindig együtt és egy irányba.
Szerkeszthető azonban egy olyan, megjegyezhető szavakból kialakuló szósor, amelyben az R vagy r illetve az L vagy l betű alatt
az adott belső két réteget értjük, az utánuk következő magánhangzó releváns és jelzi az együttes forgatás irányát, míg a
"T", "B" és "F" utáni magánhangzóknak nincs jelentősége, mert úgyis mindig félfordulat következik.
(A zárójelben lévő betűknek sincs jelentőségük, mert amúgy sem szerepelnek a forgatásokhoz használt jelölőrendszerünkben.)
A forgatássorozat memorizálható a már ismert formulával:
Rubi(n)t letörő töret. Férfi lábo(n) rú(g).
Ha a fenti forgatássorozatok rendben megtörténtek, akkor örülhetünk a kész 6x6x6-os bűvös kockánknak.

Összeállította: Straub Tamás
A leírt módszer - részben vagy egészben - a forrás megjelölésével szabadon felhasználható.
Írjon nekünk, ha a portállal vagy az oldallal kapcsolatban mondanivalója van:



