7x7x7-es bűvös kocka kirakása egyszerűen
Ha kíváncsi vagy megleled a talányokat magad
körül. Ha eltökélt is vagy megoldod azokat."
If you are curious, you'll find the puzzles around you.
If you are determined, you will solve them. (E. Rubik)
A 7x7x7-es bűvös kocka kirakása
Jelen leírás az egyik legnagyobb Rubik-kocka, a 7x7x7-es bűvös kocka kirakásáról szól. A különböző kockák megoldásáról számtalan leírás és videó található az Interneten. A jelen leírásban azoknak a kocka-kedvelőknek igyekszünk segítséget nyújtani akik már megbarátkoztak a 3x3-as illetve az 5x5-ös kockával és szeretnék egyszerűen megoldani a 7x7x7-es kockát is.
A 3x3x3-as és az 5x5-ös bűvös kockák kirakására vonatkozó módszerünk megismerésével, minimális gyakorlással (akár újabb forgatás-sorozat megtanulása nélkül) bármikor, bárki ki tudja rakni a 7x7x7-es kockát is, anélkül, hogy rendszeresen órákig kellene gyakorolnia a forgatásokat.
Tudni kell, hogy a kockát forgató versenyzők (speedcuberek), akik néhány másodperc alatt rakják ki a Rubik-kockát (a nagyobbakat is 1-2 perc alatt) több száz forgatássorozatot ismernek és az adott kockaállapothoz a megfelelőt a másodperc töredéke alatt tudják azonosítani és végrehajtani.

A forgatásokhoz használt (módosított) jelölőrendszerünk leírását és egy mini-lexikont itt találhat.
A 7x7x7-es bűvös kocka rendezésének menete:
- Először a lapközepeken található 6x25 színes kiskockákat rendezzük oldalanként egy színűre,
- majd a - rendezetlen kockán szétszórva található (12x5 db) élkockákat rakjuk szín szerint ötös csoportokba.
- A kétféle forgatássorozat eredményes befejezése
után hozzájutunk egy - lényegében - 3x3-as Rubik-kockához,
aminek a kirakását már ismerjük vagy itt megtekinthetjük.
1. Lapközepek rendezése
Itt a feladatunk az, hogy az oldalak közepén található 6x25 db egyszínű kiskockát oldalanként egy színűre, egymás mellé forgassuk. Itt is, mint a 3x3x3-as és 5x5-ös kockánál, a középen levő kiskockák meghatározták az adott oldal színét, mert egymáshoz képest állandó a helyzetük. A lapközepek hatékony rendezése érdekében azonban érdemes ismernünk a kockán lévő színek egymáshoz képesti helyzetét.
A lapközepek rendezése intuitív módon, egyszerűen megoldható, komolyabb segítséget nem igényel annak, aki már egy kis tapasztalatot szerzett a 3x3-as és 5x5-ös kockák kirakása során.
Praktikus okokból mindig azonos pl. fehér vagy citromsárga oldallal kezdjük a lapközepek rendezését, mert ezek a színek - ha jó a kocka színezése - könnyebben szembe tűnnek. Az első lapközép rendezése után a szemben levő oldal lapközepét rakjuk ki. Ezután a két kirakott lapközepes oldalnál fogjuk meg a kockát és már csak a fennmaradó négy oldal irányában forgatva a kockát rakjuk ki a további négy lapközepet. Célszerű a lapközepek kiskockáiból ötös "csíkokat" összeállítani és a fennmaradó négy oldal síkjában mozgatni, cserélgetni és rendezni a közepeket színek szerint.
A lapközepek rendezése intuitív módon megoldható annak, aki már egy kis tapasztalatot szerzett a kisebb kockákkal. Ezért ehhez nem is írunk részletes algoritmusokat. Kezdőknek gondot okozhat egy-két befejező forgatás, ezekre alábbiakban mutatunk megoldásokat:
1.1 helyzet
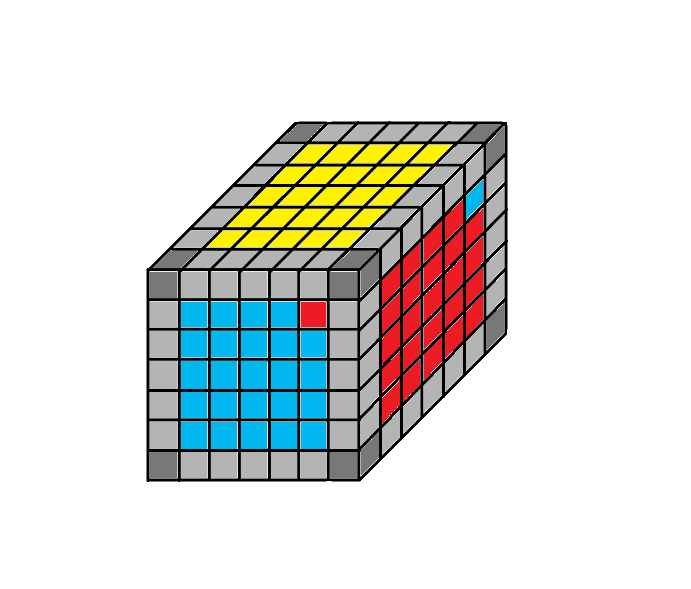
Rendező algoritmus: 2Te - Fe - 2Da - Fo - 2To - Fe - 2De
1.2 helyzet
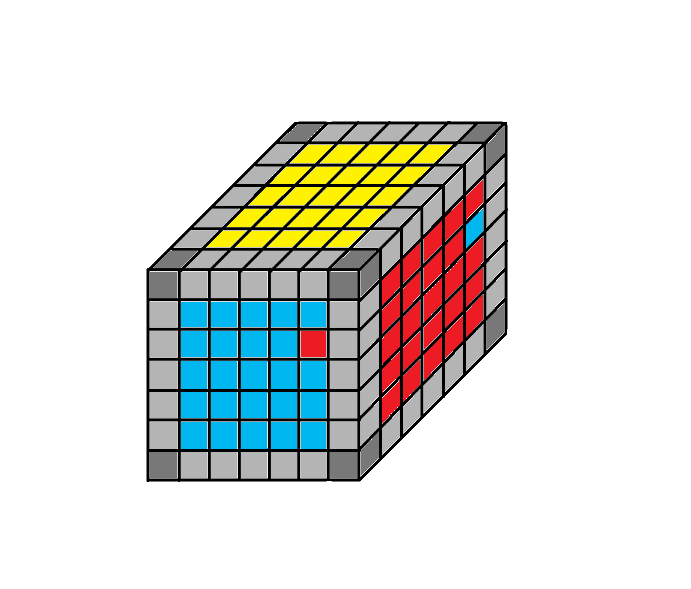
Rendező algoritmus: 3Te - Fe - 2Da - Fo - 3To - Fe - 2De
1.3 helyzet
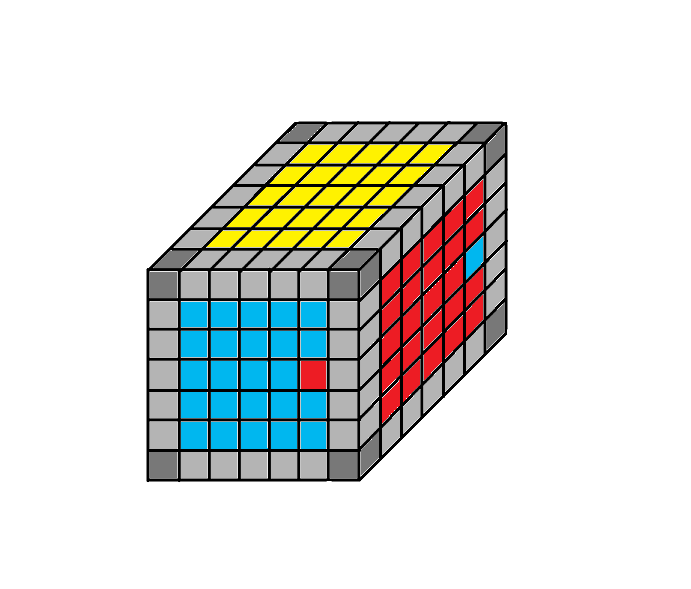
Rendező algoritmus: Ho - Fe - 2Do - Fo - He - Fe - 2De
1.4 helyzet
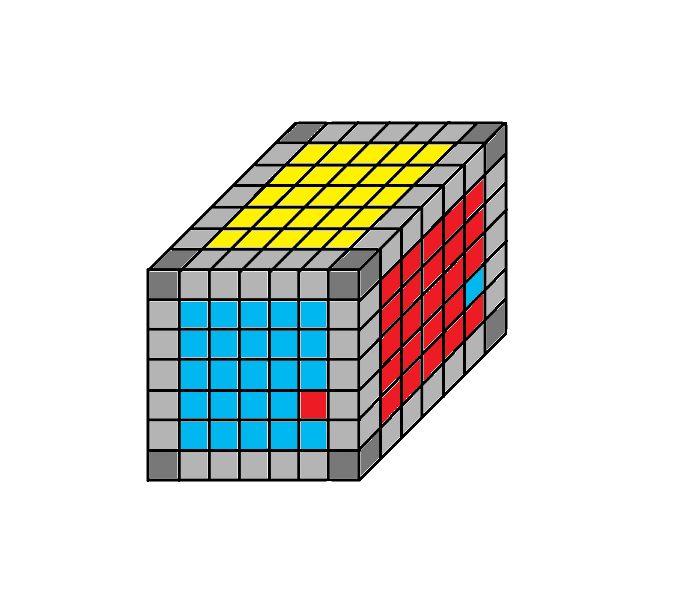
Rendező algoritmus: 3Do - Fe - 2Do - Fo - 3De - Fe - 2De
1.5 helyzet
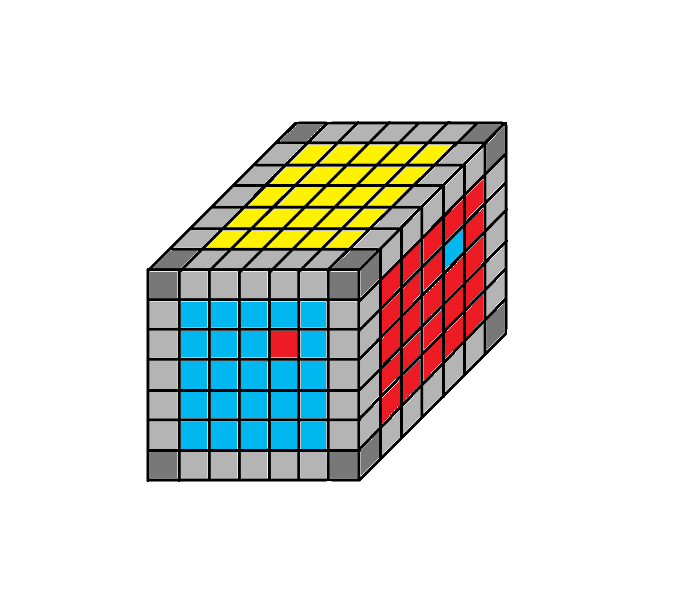
Rendező algoritmus: 3Te - Fe - 3Do - Fo - 3To - Fe - 3De
1.6 helyzet
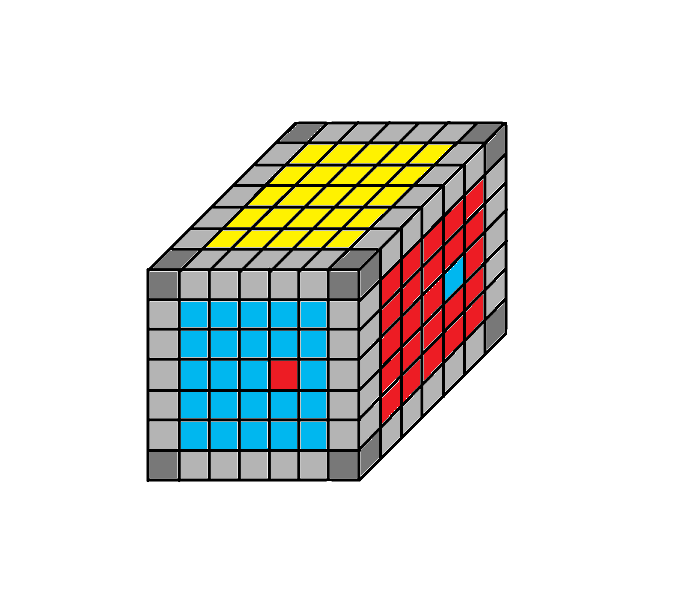
Rendező algoritmus: Ho - Fe - 3Do - Fo - He - Fe - 3De
Megjegyzés: az utolsó két lapközép intuitív rendezése során általában három-négy kiskocka megmarad, aminek szinezése a másik oldal szerinti. Ezeket egyesével a fenti algoritmusokkal rendezhetjük. Az oldalakon található 25 (pontosabban 24) közép-kiskocka bármelyike a fenti hat algoritmussal helyre hozható, csak az "F" és "R" oldal megfelelő elforgatásával be kell állítanunk az ábrán látható valamelyik induló pozíciót.
Figyeljük meg, hogy mi történik minden forgatás során: (Jelöljük a két kicserélendő kiskockát A (a piros) ill. B (a kék) betűvel.) Először a B kockát (tartalmazó réteget) az A kocka helyére visszük (1. fordítás), ezután oldalra fordítjuk és kivisszük az F oldalról a B kockával feltöltött sort (2) és (3), ezután visszafordítjuk az F oldalt (4), majd az első lépésben kiforgatott réteget is visszaforgatjuk (5), az F oldalt harmadszor is elfordítjuk (6), hogy befejezhessük a rendezést (7). Teljesen áttekinthető a folyamat, ezért egy átlagos térlátású kockaforgatónak nem is kell memorizálnia ezeket a forgatássorozatokat.
Elkészülnek tehát a lapközepek:
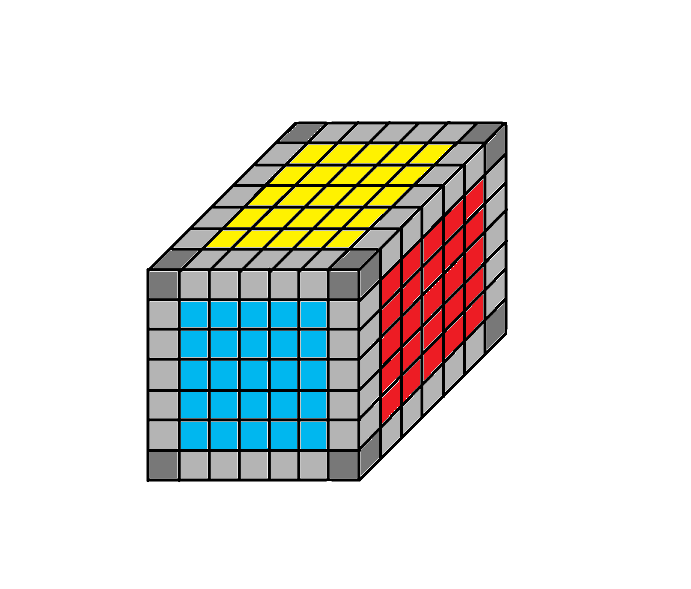
2. Élkockák rendezése
Feladatunk a rendezetlen kockán szétszórva található 12x5=60 élkocka szín szerint ötös csoportokba való rendezése. Nagyon aprólékos és igen nagy türelmet igénylő munka, de a kisebb kockák élpárosításánál megismert egyszerű és áttekinthető forgatássorozat ismételgetésével nagyrészt célt érhetünk.
Állítsuk be a két egymás mellé beforgatandó (párosítandó) élkockát úgy, hogy mindkettő a felső lapra (T) kerüljön. Egyik velünk szemben (T és F oldal találkozásánál), a másik túloldalt, a T és B oldal találkozásánál legyen. (Az ábrán a fekete színnel jelzett két élkocka.) Ügyeljünk arra, hogy a két beforgatandó élkocka színeiket tekintve megfelelő állásba kerüljön, vagyis a forgatássorozat végén a kész élkockapár színei oldalról tekintve azonosak legyenek. A forgatássorozatban mellékes szerepet játszó öt élkockának (nevezhetjük ezeket segédélkockáknak) még nem rendezett élkocka-sort válasszunk! Lásd: ábra.
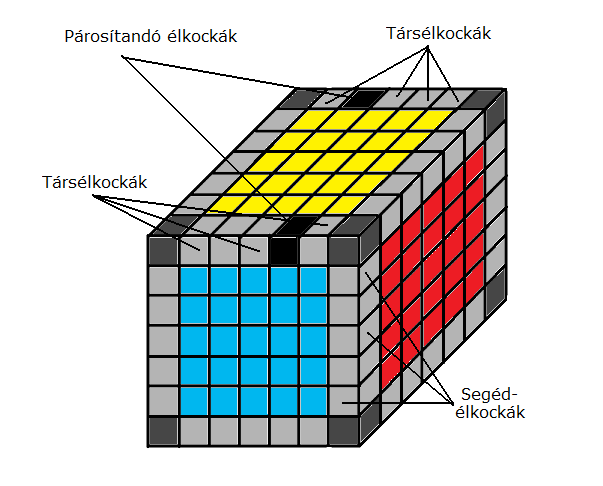
Javasolt forgatássorozat (ua., mint a kisebbeknél): 3Li-To-Ri-Ti-3Lo
Ha a T és B oldal találkozásánál levő közép-élkockát párosítanánk, akkor a forgatás-sorozat értelemszerűen: Mi-To-Ri-Ti-Ma.
Ha másik élkockát szeretnénk párosítani a forgatássorozat értelemszerűen módosul.
Az élkockák párosításának variációi még: a közelebbi élkockát visszük fel, a bal oldalon helyezzük biztonságba a
párosított élkockákat, stb.
Az élötösök rendezése során először olyan élekhez keressünk párt, amiben kettő, három vagy négy élkocka már színeiben és
orientációban is megfelelő, ha találunk ilyeneket.
A segédélkockák és az ún. társkockák színösszeállítása és orientációja függvényében egyszerre egy, kettő vagy három
élhármast tudunk rendezni.
Figyeljük meg, hogy mi történik a forgatások során: Először párosítjuk a kiválasztott élkockákat (1. fordítás), ezután oldalra visszük (2) és "biztonságba" helyezzük (3), majd miután a segédélkockák a helyükre léptek, visszafordítjuk a felső réteget (4), hogy az elmozdított lapközepeket helyre hozhassuk (5). Teljesen áttekinthető a folyamat, ezért egy átlagos térlátású kockaforgatónak nem is kell memorizálnia ezt a forgatássorozatot.
3. Élkockák rendezésének végén felmerülő paritás helyzetek
A 7x7x7-es kocka rendezése során már az élsorok kialakításánál beleütközünk paritás-helyzetekbe. A továbbiakban ezeket vesszük sorra.
3.1 Az utolsó élötös színezése nem homogén

Alkalmazandó forgatás-sorozat:
2Ru-Bu-Tu-2Le-Tu-2Ro-Tu-2Re-Tu-Fu-2Re-Fu-2Lo-Bu-2Ru
Ez az algoritmus már ismerős lehet a kisebb kockák megoldásaiból, mindazonáltal szükséges, hogy egy kicsit egyszerüsítsük és megjegyezhető alakra hozzuk, mert elég gyakran szükségünk van rá.
Vegyük észre, hogy a T, F és B oldalak mindig félfordulatot végeznek, ezen kívül csak a "2R" és az "2L" oldalak/rétegek fordulnak. Tehát - csak ebben az algoritmusban - a 2. réteget értjük az R vagy r illetve az L vagy l betű alatt. Ezen egyszerűsítések után szerkeszthető egy olyan, megjegyezhető szavakból kialakuló szósorozat, amelyben csak az R és L betűk utáni magánhangzó releváns és jelzi a forgatás irányát, míg a "T", "F" és "B" utáni magánhangzóknak nincs jelentősége, mert úgyis mindig félfordulat következik. (A zárójelben lévő betűknek sincs jelentőségük, mert amúgy sem szerepelnek a forgatásokhoz használt jelölőrendszerünkben.)
A forgatássorozat az előzőekben leírt értelmezéssel memorizálható így is:
Rubi(n)t letörő töret. Férfi lábo(n) rú(g).
(ugyanaz, mint a kisebb kockáknál)
Megjegyzés: Az algoritmus némi módosításával a másik szárnykockát is meg tudjuk helyben fordítani (2R és 2L helyett a 3R és 3L fordul).
3.2 Két élötösben egy vagy több szárnyat kell megcserélni
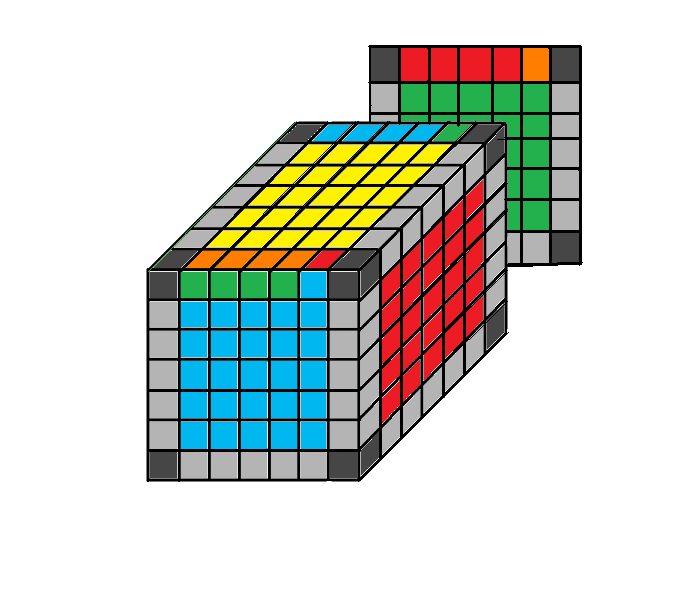
Alkalmazandó forgatás-sorozat:
(2Lo-Tu)2-Fu-2Lo-Fu-2Re-Tu-2Ro-Tu-2Lu
Az algoritmus végrehajtása eredményeként a sorba nem illeszkedő élszárnyak egymással kicserélődnek és meg is fordulnak.
A forgatássorozat az előzőekben leírt egyszerűsítésekkel (T és F oldal mindig félfordulatot végez, stb.) és
értelmezéssel memorizálható így is:
Lótu(sz), lótu(sz)-faló, fűré(sz)t ro(s)tálu(nk).
(ugyanaz, mint a kisebb kockáknál)
Megjegyzés: Az algoritmus némi módosításával a másik szárnykockát is ki tudunk egymással cserélni (2R és 2L helyett a 3R és 3L fordul).
Ha csak saját kedvünkre forgatjuk a kockát és az idő nem számít, akkor nem szükséges az itt következő paritás-helyzetekre algoritmusokat megtanulni, mert elég az előző kettőt ismerni ahhoz, hogy meg tudjuk oldani az összes paritás problémát.
3.3 Két élötösben az élközepeket kell megcserélni
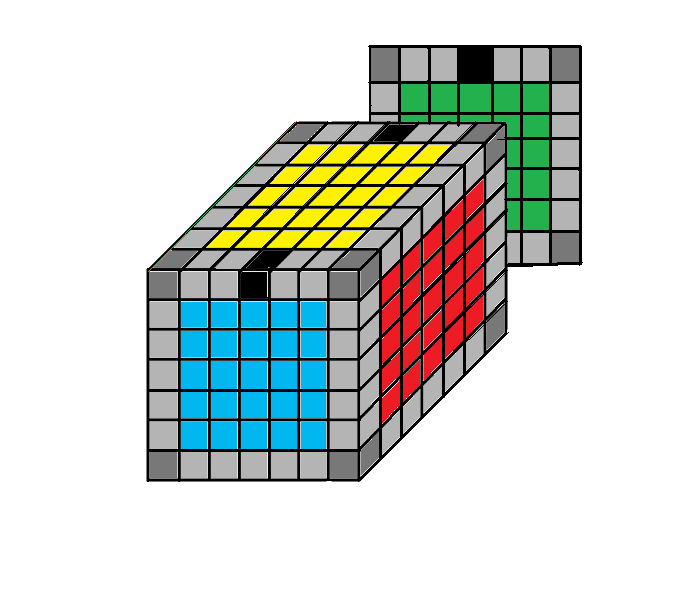
Alkalmazandó forgatás-sorozat:
2Ru3Ru-Bu-(2Ro3Ro-Tu)2-Bu-2Ro3Ro-Bu-2Re3Re-Bu-2Ro3Ro-Bu-2Ru3Ru-Bu-Tu
A forgatás-sorozat eredményeként a feketével jelzett közép-élkockák egymással kicserélődnek.
Megjegyzés: Az algoritmus végrehajtásával a közép-élkockák megfordulás nélkül helyezdődnek át, azonban "mellékhatásként" a közelebbi szárnyak egyúttal meg is fordulnak. (A kirakás ezen fázisában ez azonban semmi gondot nem okozhat.)
Ezt az algoritmust nem szükséges megtanulni, mert kiváltható kétszer végrehajtott 3.2-es forgatással, közötte az egész kocka függőleges tengelyű 180°-os transzformációjával.
A forgatássorozat az előzőekben leírt egyszerűsítésekkel (T és B oldal mindig félfordulatot végez, ezen kívül
a "2R" és "3R" illetve az "2L" és"3L" oldalak/rétegek fordulnak és mindig párjukkal együtt azonos mértékben és irányban.
Tehát - csak ebben az algoritmusban - a két réteg együttesét értjük az R vagy r illetve az L vagy l betű alatt, stb.) és
értelmezéssel memorizálható így is:
Rubi(n), rőt, rőt, bíró bére boro(k), berú(g), bete(g).
3.4 Két élötösben is meg kell fordítani elemeket helyben

A kívánt rendezés itt is megoldható kétszer végrehajtott 3.1-es forgatással, közötte az egész kocka függőleges tengelyű 180°-os transzformációjával.
4. A kocka rendezése
Az előző három fejezet végrehajtása után kialakítottunk egy lényegében 3x3x3-as Rubik-kockát,

aminek a kirakását már ismerjük vagy itt megtekinthetjük.
Talán azt nem is kell említeni, hogy ebben a befejező fázisban a 7x7-es kocka külső oldalait csak magukban, a kocka belső öt rétegét pedig együtt forgassuk.
Megjegyzés: Ebben az utolsó fázisban már nem találkozunk újabb paritáshelyzetekkel, mint ahogy az a 4x4x4-es vagy 6x6x6-os kockáknál előfordulhat.
Ha a fenti forgatássorozatok rendben megtörténtek, akkor örülhetünk a kész 7x7x7-es kockánknak.
A fent leírt módszer - részben vagy egészben - a forrás megjelölésével szabadon felhasználható.
Összeállította: Straub Tamás
Írjon nekünk, ha a portállal vagy az oldallal kapcsolatban mondanivalója van:



